Examples:

1. Find the area between these two curves:
   $$\begin{array}{l}y={\left(x-2\right)}^2+3\\ y=-3x^2+13\end{array}$$

   • Plot the curves to see where the curves intersect and to help you visualize the area between the curves. In this case, both curves are second degree polynomials. Two 2nd degree polynomials may intersect in 0, 1, or 2 points.
   • Solve for the points of intersection
   • Integrate the difference between the curves from the lower limit to the upper limit of integration.
   

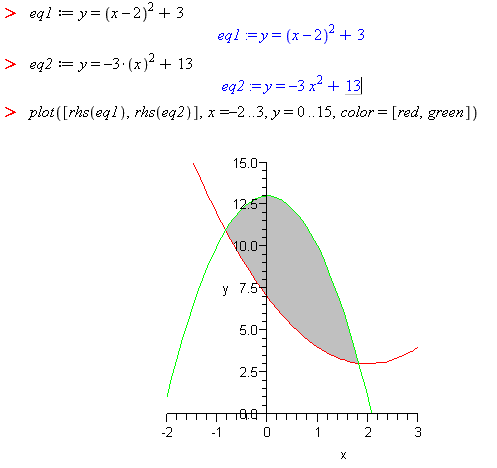
   Notice that the solve command did not work for these equations, but the allvalues was successful in completing the work to find the solution, the points of intersection.

   

2. Find the area of overlap of the two circles defined by $$\begin{array}{l}{x}^2+{\left(y-3\right)}^2=6\\ x^2+{\left(y-5\right)}^2=4\end{array}$$

   

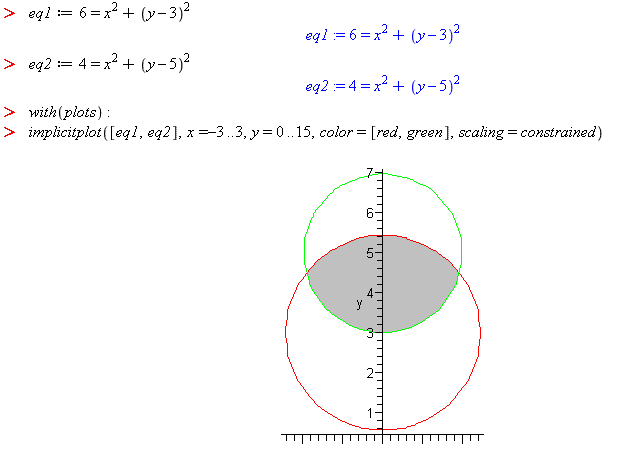
   Recall that with quadratic equations, there are two results for each point along either the x or y axis. This means additional work will be required to compute the overlap.

   To simplify the problem, symbolically solve each circle equation for y and plot only the parts of each circle that overlap.

   

   Now, solve for the points of intersection and integrate the difference (area between the curves).

   

   Note, this technique works for overlap where the intersection points can be distinguished by the x values. If the points of intersection have the same x coordinate, but different y coordinate, then solve the circle equations for x and integrate along the y-axis.